Практики

Впервые в педагогике понятие «технология» появилось на рубеже 1940–1950-х гг. и было связано с использованием в педагогическом процессе технических средств и программированного обучения.

Возникновение у учащихся интереса к изучаемому предмету и, в частности, к математике, как минимум на половину зависит от того, как будет построена методика преподавания. Задачей учителя является создание такой атмосферы, при которой как можно большая часть учеников работала бы активно, была заинтересована, настроена на познание. 

В качестве эффективных средств развития интереса к учебному предмету принято использовать такие приёмы, как: логические разминки, дидактические игры, сюжетно-ролевые игры, творческие задания, ребусы.

Применение этих процессов вовлечения и мотивации учащихся в науке получило название «геймификация образования». Под геймификацией принято понимать применение игровых методик в неигровых ситуациях.

Изучение развития детей показывает, что в игре эффективнее, чем в других видах деятельности, развиваются психические процессы, поэтому опора на игру – это важнейший путь включения школьников в учебную работу.

Игра вводит ребёнка в жизнь, в общение с окружающими, с природой, способствует приобретению знаний.
В жизни людей игра выполняет следующие функции:
1) развлекательную: основная функция игры – развлечь, доставить удовольствие, воодушевить, пробудить интерес;
2) коммуникативную: с помощью игры осваивается диалектика общения;
3) самореализации, т. к. в игре человек приобретает практические навыки;
4) терапевтическую: преодоление различных трудностей, возникающих в других видах жизнедеятельности;
5) диагностическую: выявление отклонений от нормативного поведения, самопознание в процессе игры;
6) коррекционную: внесение позитивных изменений в структуру личностных показателей;
7) межнациональной коммуникации: усвоение единых для всех людей социокультурных ценностей;
8) социализации: включение в систему общественных отношений, усвоение норм человеческого общежития.

Актуальность применения игровых технологий на уроках математики мы видим в том, что:
- игровые формы обучения на уроках создают возможности эффективной организации взаимодействия педагога и учащихся, продуктивной формы их общения с присущими им элементами соревнования;
- в игре заложены огромные воспитательные и образовательные возможности;
- игры очень хорошо уживаются с «серьёзным» учением;
- включение в урок игр делает процесс обучения интересным и занимательным, облегчает преодоление трудностей в усвоении учебного материала;
- разнообразные игровые действия, при помощи которых решается та или иная умственная задача, поддерживают и усиливают интерес к учебному предмету.

Как известно, структурными компонентами игры являются: игровой замысел, правила, сами участники игры, цели и задачи, содержание и результат; также, в частности, в математических дидактических играх компонентами будут являться оборудование (например, линейка, циркуль) и дидактическая задача. Сочетание всех элементов игры, их взаимодействие в совокупности повышают её эффективность и, как следствие, приводят к положительному результату.

Математические игры объединяют учение и игру, труд и отдых. Они развивают математические способности, сообразительность, логическое мышление, укрепляют память.

Использование программного материала вызывает у учащихся активизацию умственной деятельности, способствует возникновению личных мотивов учения. А включение заданий, которые содержат новые для учащихся сведения из различных областей математики, развивает интерес и любознательность. 

В связи с этим необходимо позаботиться о том, чтобы вовлечь учащихся в активную учебную деятельность на уроках, создавая игровые ситуации или проводя дидактические игры, которые позволят в достаточной мере, раскрепостив ученика, постепенно формировать интерес к математике, приучать к сотворчеству с товарищами и учителем. 

Применяя игровые формы, чередуя «серьезную» и «несерьезную» математику, обеспечивается на уроках устойчивое внимание к изучаемому материалу.

Цели применения математических игр:
развитие мышления;
углубление теоретических знаний;
самоопределение в мире увлечений и профессий;
организация свободного времени;
общение со сверстниками;
воспитание сотрудничества и коллективизма;
приобретение новых знаний, умений и навыков;
формирование адекватной самооценки;
развитие волевых качеств;
контроль знаний;
мотивация учебной деятельности

Задачи математических игр:
1. Образовательные:
способствовать прочному усвоению учащимися учебного материала;
способствовать расширению кругозора учащихся и др.
2. Развивающие:
развивать у учащихся творческое мышление;
способствовать практическому применению умений и навыков, полученных на уроках и внеклассных занятиях;
способствовать развитию воображения, фантазии, творческих способностей и др.
3. Воспитательные:
способствовать воспитанию развивающейся и реализующейся личности;
воспитать нравственные взгляды и убеждения;
способствовать воспитанию самостоятельности и воли в работе.

Функции математических игр:
1. Во время математической игры происходит одновременно игровая, учебная и трудовая деятельность. Действительно, игра сближает то, что в жизни не сопоставимо, и разводит то, что считается едино.
2. Математическая игра требует от обучающегося, чтобы он знал предмет. Ведь, не умея решать задачи, разгадывать, расшифровывать и распутывать, ученик не сможет участвовать в игре.
3. В играх ученики учатся планировать свою работу, оценивать результаты не только чужой, но и своей деятельности, проявлять смекалку при решении задач, творчески подходить к любому заданию, использовать и подбирать нужный материал.
4. Результаты игр показывают школьникам их уровень подготовленности. Математические игры помогают в самосовершенствовании учащихся и тем самым побуждают их познавательную активность, повышается интерес к предмету.
5. Во время участия в математических играх учащиеся не только получают новую информацию, но и приобретают опыт сбора нужной информации и правильного её применения.

Требования к игровым урокам

К участникам математической игры должны предъявляться определенные требования в отношении знаний, в частности: чтобы играть, надо знать. Это требование придает игре познавательный характер.
Правила игры должны быть такими, чтобы учащиеся проявили желание поучаствовать в ней. Поэтому игры должны разрабатываться с учетом возрастных особенностей детей, проявляемых ими интересов в том или ином возрасте, их развития и имеющихся знаний.
Математические игры должны разрабатываться с учетом индивидуальных особенностей учащихся, с учетом различных групп учащихся: слабые, сильные; активные, пассивные и др. Они должны быть такими, чтобы каждый тип учащихся смог проявить себя в игре, показать свои способности, возможности, свою самостоятельность, настойчивость, смекалку, испытать чувство удовлетворенности, успеха.
При разработке игры нужно предусмотреть более легкие варианты игры, задания для слабых учащихся и, наоборот, более сложный вариант для сильных учеников. Для совсем слабых учащихся разрабатываются игры, где не нужно думать, а нужна лишь смекалка.
Математические игры должны разрабатываться с учетом предмета и его материала. Они должны быть разнообразны. Многообразие видов математических игр поможет повысить эффективность урока математики, послужит дополнительным источником систематических и прочных знаний.
Таким образом не только сильные учащиеся проявляют интерес к предмету, но и слабые учащиеся начинают проявлять свою активность в учении.

При организации игровой формы урока необходимо придерживаться следующих положений:
1. Правила игры должны быть простыми, точно сформулированными, а математическое содержание предлагаемого материала – доступно пониманию обучающихся. В противном случае игра не вызовет интереса и будет проводиться формально.
2. Игра должна давать достаточно пищи для мыслительной деятельности, в противном случае она не будет содействовать выполнению педагогических целей, не будет развивать математическую зоркость и внимание.
3. Дидактический материал, используемый во время игры, должен быть удобен в использовании, иначе игра не даст должного эффекта.
4. При проведении игры, связанной с соревнованиями команд, должен быть обеспечен контроль над её результатами со стороны всего коллектива учеников или выбранных лиц. Учёт результатов соревнования должен быть открытым, ясным и справедливым.
5. Каждый ученик должен быть активным участником игры. Длительное ожидание своей очереди для включения в игру снижает интерес детей к игре.
6. Игровой характер при проведении уроков по математике должен иметь определённую меру. Превышение этой меры может привести к тому, что дети во всём будут видеть только игру.
7. В процессе игры учащиеся должны математически грамотно проводить свои рассуждения, речь их должна быть правильной, чёткой, краткой.

Виды математических игр:
игры-упражнения;
игры-путешествия;
сюжетная ролевая игра:
игра-соревнование.

Игры-упражнения занимают обычно 10–15 минут и направлены на совершенствование познавательных способностей учащихся, осмысление и закрепление учебного материала, Это разнообразные викторины, кроссворды, ребусы, шарады, головоломки, загадки.
Игры-путешествия служат в основном целям углубления, осмысления и закрепления учебного материала.
Сюжетная игра отличается тем, что инсценируются условия воображаемой ситуации, а учащиеся играют определённые роли.
Игра-соревнование. Существенной особенностью игры-соревнования является наличие в ней соревновательной борьбы и сотрудничества. Элементы соревнования занимают ведущее место в основных игровых действиях, а сотрудничество, как правило, определяется конкретными обстоятельствами и задачами.
Игра-соревнование позволяет учителю в зависимости от содержания материала вводить в игру не просто занимательный материал, но весьма сложные вопросы учебной программы.

Пожалуй, одной из самых известных игр является «Морской бой». Однако мало кому известно, что даже такую простую игру можно использовать в образовательных целях. Так, с помощью неё ученики быстро могут освоить такую тему, как «Координаты точки на плоскости». В процессе данной игры учащиеся убеждаются, что положение точки на плоскости определяется с помощью двух её координат, при этом система отсчёта у каждого игрока должна быть одинакова для того, чтобы возможно было играть. Помимо способствования лёгкому усвоению математического материала, эта игра развивает также немаловажные тактические навыки ученика: внимательность, наблюдательность, сообразительность, терпение и выдержку. Всё это будет полезно не только на уроке математики, но может пригодиться и в жизни.

Игра «Соревнование художников»
На доске записаны координаты точек: (0; 0), (-1; 1), (-3; 1), (-2; 3), (-3; 3), (-4; 6), (0; 8), (2; 5), (2; 11), (6; 10), (3; 9), (4; 5), (3; 0), (2; 0), (1; -7), (3; -8), (0; -8), (0; 0).
Отметить на координатной плоскости каждую точку и соединить с предыдущей при помощи отрезка. Результат – определенный рисунок. Эту игру можно провести с обратным заданием: нарисовать самим любой рисунок, имеющий конфигурацию ломаной и записать координаты вершин.
Эти игры развивают внимание, наблюдательность, сообразительность, ученики быстрее усваивают матеріал и убеждаются, что положение точки на плоскости определяется с помощью двух её координат.

Игра «Математическое лото»
Каждому ученику выдается конверт, в котором 1 большая карта с заданиями и маленькие (их больше, чем заданий). На маленьких – результаты вычислений. Ученик должен выполнить задание на большой карте и накрыть его ответом (результатом его вычислений). После выполнения всех заданий ученик переворачивает маленькие карточки и получает задание (если верно выполнены все вычисления). Например: определение целых чисел, правило сравнения, правило сложения, вычисление, деление, умножения целых чисел и др. Затем ученики выполняют полученные задания.

Игра «Магические квадраты»
1. В клетки квадрата записать такие числа, чтобы сумма чисел по любой вертикали, горизонтали была равна 0.

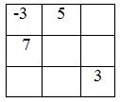
2. Записать в клетки квадрата числа -1; 2; -3; -4; 5; -6; -7; 8; -9 так, чтобы произведение по любой диагонали, вертикали и горизонтали было равно положительному числу.

Игра «Забег по кругу»

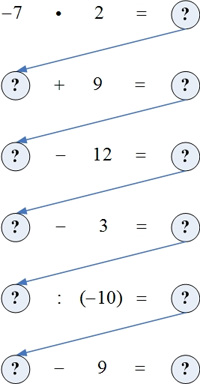
На доске записана цепочка примеров, которые нужно выполнить строго по направлению стрелки. При правильном выполнении заданий получают первое число цепочки.

Эти игры помогают усвоить все действия с целыми числами, вырабатывать вычислительные навыки, сообразительность, внимательность.

Тема «Десятичные дроби»
Игра «Цветочек»
В листе цветка помещается дробь, которую нужно сложить, умножить, разделить, вычесть. Дроби, с которыми нужно произвести эти действия, записаны на лепестках цветка.

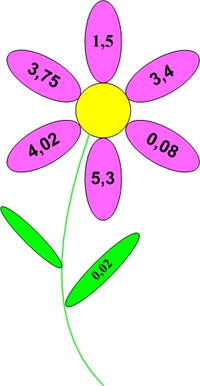
1) 1,5 ∙ 0,02
2) 3,75 ∙ 0,02
3) 3,4 : 0,02
4) 0,08 + 0,02
5) 4,02 + 0,02
6) 5,3 – 0,02

После того, как ученики выполнят указанные действия, тот, кто первым выполнит все вычисления, рисует на доске такой же цветок, только в лепестках пишет результаты вычислений.

Тема «Признаки делимости чисел»
Игра «Лучший счетчик»
Класс делится на три команды. Каждая выбирает «счетчика», который будет защищать свою команду. Примеры «счетчику» задают члены других команд до тех пор, пока он не собьется. Затем его сменяет «счетчик» другой команды. За каждый правильный ответ команда получает 1 очко. Побеждает команда, которая набрала больше очков. Условие игры – отвечать на вопросы быстро.

В ходе игры вырабатывается быстрота вычислений, внимательность, сообразительность.

Основным в дидактической игре на уроках математики является обучение математике. Игровые ситуации лишь активизируют деятельность учащихся, делают восприятие более активным, эмоциональным, творческим. Создание игровых ситуаций на уроках повышает интерес к предмету, вносит разнообразие и эмоциональную окраску в учебную работу, снижает утомление, развивает внимание, взаимопомощь.

Тема «Действия с рациональными числами»
Игра «Брейн-ринг»
Применяется при закреплении или повторении темы. В игре принимают участие 4 команды. Команды начинают решать задания одновременно после сигнала учителя. Команда, которая первой выполняет задание, звонит в колокольчик. Первые две команды, ответившие правильно, получают по 1 баллу. За нарушение дисциплины баллы снимаются. Каждая команда после ответа собирает карточки и сдаёт на проверку, затем получает новое задание. Время выполнения задания – 2 минуты. Задания подбираются по определённой теме урока.

Дидактические игры
Дидактические игры влияют на повышение качества знаний, умений и навыков учащихся, развитие умственной деятельности. Условно можно выделить несколько типов дидактических игр, сгруппированных по виду деятельности учащихся:

Игры-путешествия. Имеют сходство со сказкой, её развитием, чудесами. Игра-путешествие отражает реальные факты или события, но обычное раскрывается через необычное, простое – через загадочное, трудное – через преодолимое, необходимое – через интересное. Все это происходит в игре, в игровых действиях, становится близким ребенку, радует его. Цели игры-путешествия: усилить впечатление, придать познавательному содержанию чуть-чуть сказочную необычность, обратить внимание детей на то, что находится рядом, но не замечается ими. Игры-путешествия обостряют внимание, наблюдательность, осмысление игровых задач, облегчают преодоление трудностей и достижение успеха. Игры-путешествия всегда несколько романтичны. Именно это вызывает интерес и активное участие в развитии сюжета игры, обогащение игровых действий, стремление овладеть правилами игры и получить результат: решить задачу, что-то узнать, чему-то научиться. Роль педагога в игре сложна, требует знаний, готовности ответить на вопросы детей, играя с ними, вести процесс обучения незаметно. Например, «Путешествие в страну дробей», «Космическое путешествие (площади и объемы фигур)», «Веселый математический поезд».

Игры-поручения. Имеют те же структурные элементы, что и игры-путешествия, но по содержанию они проще и по продолжительности короче. В их основе лежат действия с предметами, игрушками, словесные поручения. Игровая задача и игровые действия в них основаны на предложении что-то сделать: «Помоги Буратино расставить знаки в примерах», «Проверь домашнее задание у Незнайки».

Игры-предположения. «Что было бы…?» или «Что бы я сделал…», «Как я решил и почему?» и др. Иногда началом такой игры может послужить картинка, задание, задача, проблема. Дидактическое содержание игры заключается в том, что перед детьми ставится задача и создается ситуация, требующая осмысления последующего действия. Игровая задача заложена в самом названии: «Что было бы…?» или «Что бы я сделал…». Игровые действия определяются задачей и требуют от детей целесообразно предполагаемого действия в соответствии с поставленными условиями или созданными обстоятельствами. Дети высказывают предположения, констатирующие или обобщенно-доказательные. Эти игры требуют умения соотнести знания с обстоятельствами, установления причинных связей. В них содержится и соревновательный элемент: кто быстрее сообразит.

Игры-загадки. Педагогическая направленность загадок заключается в проверке знаний учащихся. В настоящее время загадки, загадывание и отгадывание рассматриваются как вид обучающей игры. Основным признаком загадки является замысловатое описание, которое нужно расшифровать (отгадать и доказать). Описание это лаконично и нередко оформляется в виде вопроса или заканчивается им. Главной особенностью загадок является логическая задача. Способы построения логических задач различны, но все они активизируют умственную деятельность ребенка. Детям нравятся игры-загадки. Необходимость сравнивать, припоминать, думать, догадываться доставляет радость умственного труда. Разгадывание загадок развивает способность к анализу, обобщению, формирует умение рассуждать, делать выводы, умозаключения.

Игры-беседы (игры-диалоги). В основе игры-беседы лежит общение педагога с детьми, детей с педагогом и детей друг с другом. Это общение имеет особый характер игрового обучения и игровой деятельности детей. В игре-беседе учитель часто идет не от себя, а от близкого детям персонажа, и тем самым не только сохраняет игровое общение, но и усиливает радость от него, желание повторить игру. Однако игра-беседа таит в себе опасность усиления приемов прямого обучения. Ценность игры-беседы заключается в том, что она предъявляет требования к активизации эмоционально-мыслительных процессов: единства слова, действия, мысли и воображения детей. Игра-беседа воспитывает умение слушать и слышать вопросы учителя, вопросы и ответы детей, умение сосредоточивать внимание на содержании разговора, дополнять сказанное, высказывать суждение.

Игра «Космическая прогулка»
Основная цель игры — отработать умения и навыки применения правил умножения десятичных дробей. Помимо этого, игра должна осуществить контроль знаний учащихся, развить их любознательность и коммуникацию. Класс разбивается на 3 группы, каждая группа – экипаж космического корабля. У каждого ученика есть путевой лист, в котором он записывает результаты и решение всех примеров, встречающихся в течение урока. Игра состоит из трех этапов: составление девиза урока, расчёт пути планет и расчёт площади посадочной полосы. На 1-м этапе учащиеся должны восстановить слова В. Чкалова «Полёт — это математика», решив следующие примеры и записав ответы в таблицу:

1) 2,5 · 0,3 = 0,75 (П)
2) 1,2 · 4 = 4,8 (О)
3) 7 · 0,8 = 5,6 (Л)
4) 2,1 · 0,01 = 0,021 (Ё)
5) 3,7 · 10 = 37 (Т)
6) 5,4 · 0,02 = 0,108 (Э)
7) 0,37 · 100 = 37 (Т)
8) 20 · 0,24 = 4,8 (О)
9) 1,3 · 3,2 = 4,16 (М)
10) 1,5 · 0,8 = 1,2 (А)
11) 3700 · 0,01 = 37 (Т)
12) 100 · 0,1 = 10 (Е)
13) 20,8 · 0,2 = 4,16 (М)
14) 4 · 0,3 = 1,2 (А)
15) 74 · 0,5 = (Т)
16) 7,5 · 1,6 = 12 (И)
17) 0,4 · 1,04 = 0,056 (К)
18) 6 · 0,2 = 1,2 (А)

Таблица 1

На 2-м этапе учащиеся должны решить задачу: Скорость планеты Меркурий 47,8 км/с, а скорость планеты Венера на 12,8 км/с меньше. Какой путь проходит Меркурий за 3 с, а Венера за 10,2 с?

Решение:
47,8 - 12,8 = 35 (км/с) – скорость планеты Венера; 47,8 · 3 = 143,4 (км) – проходит планета Меркурий за 3 с; 10,2 · 35 = 357 (км) – проходит планета Венера за 10,2 с. Ответ: 143,4 км, 357 км.

На 3-м этапе ученики должны «посадить» космический корабль, рассчитав периметр и площадь посадочной площадки, которая является квадратом со стороной, равной 2,3 км Решение: Р = 2,3 · 4 = 9,2 (км), S = 2,3 · 2,3 = 5,29 (км2).

Игра «Веселый математический поезд»
Каждая команда получает свой маршрутный лист, на первой странице которого указан порядок прохождения станций. По сигналу команды расходятся по своим станциям. Время пребывания на каждой станции – 5 минут. По мере того, как команда пребывает на ту или иную станцию, дежурный по станции (педагог) заполняет маршрутный лист и выставляет баллы.
Команды отправляются по станциям.

1-я станция «Загадки»
На этой станции педагог читает задачи. Но задачи надо слушать внимательно, их решить и ответить на вопрос. За каждую решенную задачу присуждается 1 балл.

Задачи:
1. За книгу заплатили 1 руб. и ещё полстоимости книги. Сколько стоит книга? (2 руб.)
2. Тройка лошадей пробежала путь 30 км. Сколько пробежала каждая лошадь? (30 км)
3. В семье 5 сыновей, и у каждого есть сестра. Сколько детей в этой семье? (6)
4. Как одним мешком пшеницы, смолов её, наполнить два таких же мешка? (Надо в один пустой мешок вложить еще один и наполнить его пшеницей.)
5. Петух, стоя на одной ноге, весит 3 кг. Сколько он весит, стоя на двух ногах? (3 кг)
6. Катались 2 сына на трёхколёсных велосипедах, и их отец – на двухколёсном велосипеде. Сколько всего было колёс?(8)
7. Сколько концов у трех палок? А у трех с половиной? (6 и 8)
8. К однозначному числу приписали такую же цифру. Во сколько раз увеличилось число? (В 11 раз)
9. На грядке сидят 6 воробьев. К ним прилетели еще 5. Кот подкрался и схватил еще одного воробушка. Сколько осталось воробьев на грядке? (Ни одного)
10. Электровоз идет на запад со скоростью 60 км/ч. Дует восточный ветер со скоростью 40 км/ч. В каком направлении отклоняется дым от поезда, и какова его скорость? (У электровоза нет дыма.)

2-я станция «Логическая»
«Переправа через реку»
На этой станции предлагается задача на переправу через реку. За правильно решенную задачу присуждается 3 балла.
Отец с двумя сыновьями отправился в поход. На их пути встретилась река, у берега которой находился плот. Он выдерживает на воде или отца, или двух сыновей. Как переправиться на другой берег отцу и сыновьям?
(Вначале переправляются оба сына. Один из сыновей возвращается обратно к отцу. Отец перебирается на противоположный берег к сыну. Отец остается на берегу, а сын переправляется на исходный берег за братом, после чего они оба переправляются к отцу.)

3-я станция «Музыкальная»
На этой станции каждая команда должна спеть песню, в которой есть числительные. Учитывается качество исполнения песни. За каждую песню присуждается 1 балл. Количество баллов в маршрутный лист записывает старшеклассник.
Примеры песен: «Вместе весело шагать», «…Учат в школе», «Дважды два четыре».

4-я станция «Сообразительная»
На этой станции предлагается задача на сообразительность, за задачу – 3 балла.
Коля, Боря, Вова и Юра заняли первые места в соревновании. На вопрос, кто какое место занял, ребята ответили:
- Коля ни первое, ни четвертое.
- Боря занял второе место.
- Вова не был последним из четырех.
Кто какое место занял? (1-е – Вова, 2-е – Боря, 3-е – Коля, 4-е –Юра)

5-я станция «Волшебные спички»
На этой станции следует выполнить следующее задание:
Положили пять спичек. Как прибавить к ним ещё пять спичек, чтобы получилось «три»? За верно выполненное задание – 4 балла.

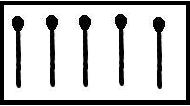
Ответ: (Рисунок).

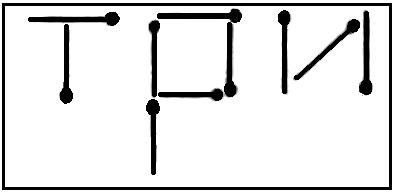
6-я станция «Эрудит»
Здесь команда должна выполнить следующее задание:
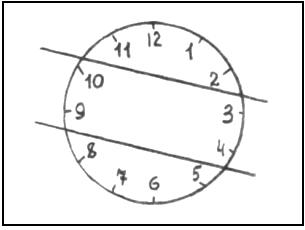
Разделить круглый циферблат часов двумя прямыми линиями на 3 части так, чтобы, сложив числа в каждой части, получить одинаковые суммы. За верно выполненное задание предлагается 3 балла.

Ответ: (Рисунок).

7-я станция «Кроссвордная»
На этой станции команде предлагается разгадать кроссворд. Разгадав его, вы прочитаете по вертикали имя великого греческого ученого. И за каждое угаданное слово – 1 балл.

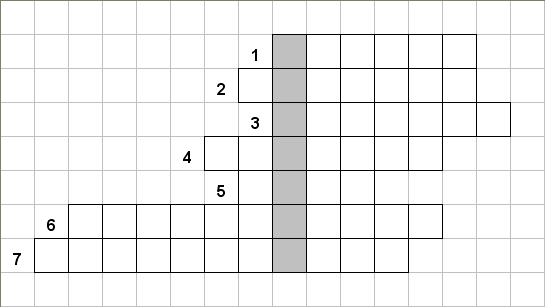
Ответ: Пифагор.

По горизонтали:
1. Угол 90 градусов. (Прямой)
2. Самая большая хорда. (Диаметр)
3. Правило, записанное с помощью букв. (Формула)
4. Прямоугольник, у которого все стороны равны. (Квадрат)
5. Геометрическая фигура, образованная двумя лучами, исходящими из одной точки. (Угол)
6. Инструмент для измерения величины углов. (Транспортир)
7. Луч, который делит угол пополам. (Биссектриса)

8-я станция « Ребусная»
Здесь команде предлагается решить два ребуса. За каждый ребус – по 3 балла.

Ответ: точка.

Ответ: Чиполлино.

9-я станция « Рыболовная»
На этой станции команде предлагаются следующие задачи про рыбок. За каждую решенную задачу – по 2 балла.
1. Два рыбака поймали 40 окуней, причем первый на 6 штук больше второго. Сколько окуней поймал каждый? (17 и 23)
2. «Какой улов был у тебя вчера?» – спросил сосед соседа-рыбака. «Я поймал два крупных леща и щуку общим весом 15 кг. Щука хороша! Она тяжелее каждого леща в 3 раза». Сколько же весит щука? (9 кг)
3. «Ну как клюет?» – спросил один рыбак второго. «Да, 9 штук сорог и окуней! Причем сорог в два раза больше! А у тебя?» – «А у меня улов почти такой же, лишь окуней на два больше». Сколько окуней у рыбаков? (8 окуней)
4. Щука вчетверо тяжелее окуня, но на 2 кг легче судака. Если к весу всех троих прибавить вес корзины, в которой они лежат – 1 кг 250 г, то получится 10 кг. Определите вес каждой рыбы в отдельности.(750 г, 3 кг, 5 кг)
5. Мальчик поймал 20 ершей и окуней, причем окуней в 3 раза меньше, чем ершей. Сколько ершей? (15 ершей)

10-я станция « Русская народная»
На этой станции команде нужно вспомнить как можно больше пословиц, поговорок, сказок, в которых используются числа. За каждую пословицу присуждается по 1 баллу.

«Пословицы о числах»
1. Одним махом семерых убивают.
2. Один с сошкой, семеро с ложкой.
3. Семь бед – один ответ.
4. Лук от семи недуг.
5. Сам не дерусь, семерых не боюсь.
6. Семеро одного не ждут.
7. Семь раз отмерь, один раз отрежь.
8. Один ум хорошо, а два лучше.
9. За двумя зайцами погонишься, ни одного не поймаешь.

11-я станция «Поздравительная»
На эту станцию приходят все команды одновременно. Жюри объявляет результаты и проводится награждение команд.

Игровые технологии являются одной из уникальных форм обучения, которая позволяет сделать интересными и увлекательными не только работу учащихся на творческо-поисковом уровне, но и будничные шаги по изучению предмета математики. Другой положительной стороной игры является то, что она способствует использованию знаний в новой ситуации, таким образом усваиваемый учащимися материал проходит через своеобразную практику, вносит разнообразие и интерес в учебный процесс.

Для учащихся нестандартный урок — переход в иное психологическое состояние, это другой стиль общения, положительные эмоции, ощущение себя в новом качестве; это возможность каждому проявить себя, развить свои творческие способности и личные качества. Задача учителя – организовать процесс обучения таким образом, чтобы каждое усилие по овладению знаниями протекало в условиях развития познавательных способностей учащихся, формирования у них таких основных приёмов умственной деятельности, как: анализ, синтез, абстрагирование, обобщение, сравнение. Игровые технологии используются на уроках в следующих случаях: в качестве самостоятельной технологии для освоения понятия, темы или даже раздела учебного предмета; как элемент более обширной технологии; в качестве урока или его части; как технология внеклассной работы.

1. Бобровский, А. А. О применении игровых технологий на уроке математики / А. А. Бобровский, З. А. Бобровская. — Текст : непосредственный // Актуальные вопросы современной педагогики : материалы IX Междунар. науч. конф. (г. Самара, сентябрь 2016 г.). — Самара : ООО «Издательство АСГАРД», 2016. — С. 1–4. — URL: https://moluch.ru/conf/ped/archive/206/10990/ (дата обращения: 10.01.2022).